Des matheux dans la salle ?

@bilpou(te):
Pour un point particulier, tu as sans doute raison, mais il y a des méthodes plus puissantes pour démontrer la continuité, il me semble (Oui, pour moi, c'est un peu plus ancien. ).
Et ensuite on peut calculer une limite...inutile...mais c'est la def de la limite.
Bien d'accord avec ton second message, j'essayais de trouver des excuses au prof.
Elle est en première année après bac.

Neo_Dogo a écrit:Si f(x0) = L ben en x0 c'est plus une limite, c'est sa valeur vraie.

C'est pas incompatible.
Un carré est un aussi rectangle.

Neo_Dogo a écrit:Mesdames & Messieurs bonjour ;
Bien OK sauf que, en principe , on ne cherche la limite que s'il y a absence de définition de la fonction, sinon on s'emmerde pas, elle a une valeur.
Pascal

Oh que si, et des exemples, il y en a une palanquée. Une fonction, elle peut être continue, ou non, dérivable ou non (et après, on parle de classe, continue et dérivable, et on peut cumuler), et tout ça sur son ensemble de définition.

Neo_Dogo a écrit:Mesdames & Messieurs bonjour ;
Les inégalités strictes sont justement utilisées pour borner les fonctions à leur Domaine.
Pascal

Non, elles sont utilisées parce que toutes les fonctions ne sont pas continues, même si elles sont définies.

Neo_Dogo a écrit:
Ben là j'suis moyen OK, vu que la fonction est définie donc c'est pas une limite, on a une valeur au point. cf mon intro ... non
Pascal

Non… cf mon poste précédent, la valeur au point peut ne pas être la même que la limite en ce point

Neo_Dogo a écrit:
Pi pas la peine de donner des fonctions "évoluées" dans ton exemple, ça marche aussi avec f(x)=x ....
Pascal

Oui, c'est vrai, mais sin(x)/x est une question courante (en terminale il y a 15 ans du moins) pour sa limite en 0 et que c'est plus facile de faire le calcul de la limite quand on connaît l'astuce

La def d'une limite c'est pourtant bien une valeur vers laquelle on tend sans pour autant jamais l'atteindre non ?
Clair que la continuité .... f(x) =1/x n'a pas vraiment la même limite à gauche et à droite de 0.

Bon aller, je lâche l'affaire, c'est trop loin pour moi tout ça. Je retourne torturer du bestiau, c'est plus simple.

Pascal

Marco66 a écrit:@bilpou(te):
Pour un point particulier, tu as sans doute raison, mais il y a des méthodes plus puissantes pour démontrer la continuité, il me semble (Oui, pour moi, c'est un peu plus ancien. ).
Et ensuite on peut calculer une limite...inutile...mais c'est la def de la limite.

Oui il y a des méthodes plus puissantes, plus rapides, etc..., mais en fait, c'est la définition initiale de la continuité en un point :
pour qu'une fonction soit coninue, limite à gauche = limite à droite = valeur au point. et j'ai envie de dire "point". Le reste, c'est des techniques de simplification (dire que x->x est continue sur R et que x->x² aussi, donc x +x² est continue sur R, c'est une méthode rapide, mais qui part du principe qu'on sait déjà prouver que x->x est continue.
Dire que comme elle est définie en x0 et qu'elle est continue en x0, sa limite vaut x0, c'est comme dire que puisque la dérivée existe, la fonction est dérivable, c'est prendre le problème à l'envers (le problème, c'est que ça marche dans 99% des cas, mais en prépa, c'est le 1% restant qu'on étudie).
Les méthodes puissantes sont quand même basées sur le fait qu'on considère acquises certaines choses.

Première année après bac, MPSI ou équivalent ?
cela dit, cours en anglais, elle est en Angleterre, ou elle est sur un cursus particulier ?

Neo_Dogo a écrit:La def d'une limite c'est pourtant bien une valeur vers laquelle on tend sans pour autant jamais l'atteindre non ?

Bonjour

Non, pas tout à fait, justement. si on pose f(x) = 0 sur R, la limite en +l'infini, c'est 0. La limite (finie) c'est effectivement une valeur vers laquelle on tend, mais on peut l'atteindre. Le truc, c'est que l'exercice, c'est toujours de calculer une limite à un endroit où la fonction n'est pas définie, parce que c'est là que c'est difficile/intéressant. Mais des limites, il y en a une infinité sur un ensemble de définition, en fait, il y en a en tout point.

AH les limites



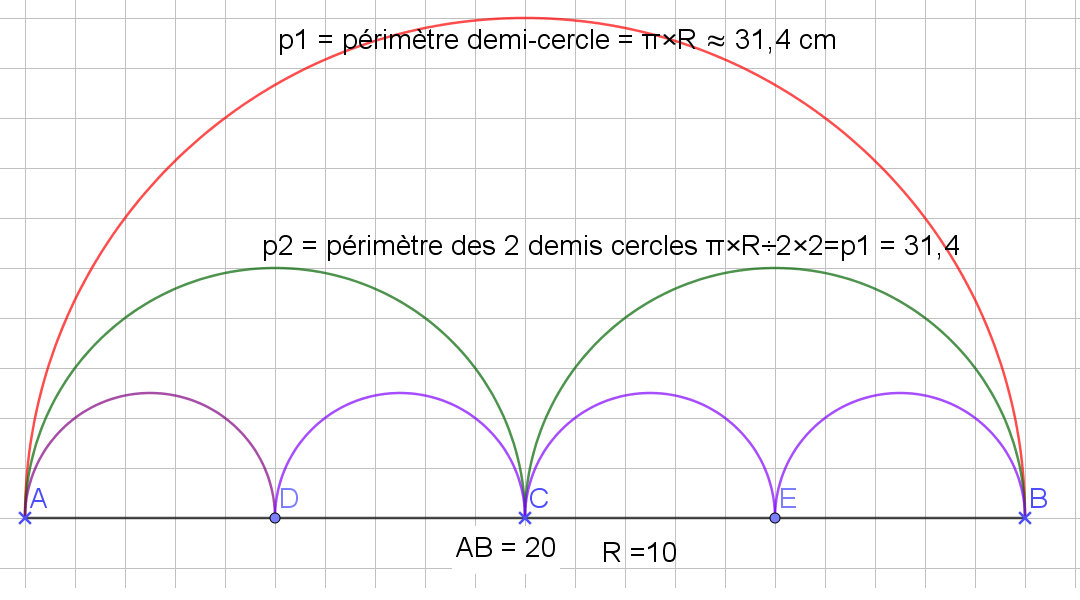
Si on continue à l'infini la division des demi-cercles ils sont confondu avec le segment AB donc 31,4 =20....

Limite n--> inf  pn = 20 ?? alors que p1 = p2= ...= p1000 =... =31,4

vous avez 20 min

Smalldave a écrit:AH les limites



Si on continue à l'infini la division des demi-cercles ils sont confondu avec le segment AB donc 31,4 =20....

Limite n--> inf  pn = 20 ?? alors que p1 = p2= ...= p1000 =... =31,4

vous avez 20 min

Tiens, je ne le connaissais pas celui-là (cela dit, là, on est dans les suites, alors l'ensemble de définition… cela dit, il faut aussi vérifier l'existence de la suite à partir de n0...)

Salut à tous.....euh Pi c est 3,14 et pas 31,4 non

Joli ! mais effectivement, c'est une suite ...
Ben vi : Pn = Pi x R x n/n  donc logiquement Pn = Pi x R et ce qqsoit n.
Faut juste avoir un point de départ avec n0.

Bon une classique parmi les classiques :
A = B   .................... on va multiplier des deux côtés par A
A2 = AB  .................... on retranche B2 des deux côtés
A2 - B2 = AB - B2 ..................oh ... une identité remarquable ...
(A-B) (A+B) = B (A-B)  .................. on simplifie pour y voir plus clair
(A+B) = B  .............................. on peut remplacer A par B puisque A = B
A+A = A
Donc 2A = A
Si on pose A=1 ....

Pascal

Edit pour Lolo : oui mais comme tu le multiplies par R qui vaut 10 ...
Pi j'avais pas fini la dém .... sorry pour ceux qui veulent suivre

Neo_Dogo a écrit:Joli ! mais effectivement, c'est une suite ...
Ben vi : Pn = Pi x R x n/n  donc logiquement Pn = Pi x R et ce qqsoit n.
Faut juste avoir un point de départ avec n0.

Bon une classique parmi les classiques :
A = B
A2 = AB
A2 - B2 = AB - B2
(A-B) (A+B) = B (A-B)
(A+B) = B
Si on pose A=1 ....

Pascal

Edit pour Lolo : oui mais comme tu le multiplies par R qui vaut 10 ...

Je l'ai sur un t-shirt, celle-là (je la dévoile pas à ceux qui ne connaissent pas)

bilou(te) a écrit:Dire que comme elle est définie en x0 et qu'elle est continue en x0, sa limite vaut x0, c'est comme dire que puisque la dérivée existe, la fonction est dérivable, c'est prendre le problème à l'envers (le problème, c'est que ça marche dans 99% des cas, mais en prépa, c'est le 1% restant qu'on étudie).

C'est pas faux et je me range à ton approche.
Ma fille est dans une section particulière d'une école à Lyon après un bac "section internationale américaine" à Nantes.

@Pascal: elle est bien celle-là et compréhensible avec un petit niveau de math.
@Smalldave : je connaissais pas non plus. Pas mal.

Pour moi ce sera un Doliprane...merci!
Jean-Paul